Data
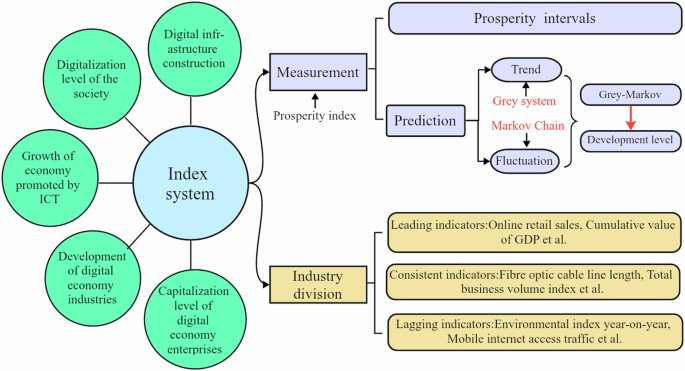
This study selects 23 indicators from five aspects: digital infrastructure construction, digitalization level of society, growth of the economy promoted by ICT, development of digital economy industries, and capitalization level of digital economy enterprises. The data is selected from the China Stock Market & Accounting Research Database (CSMAR) over the period from Q2 2017 to Q2 2023. A detailed summary of the variables is presented in Table 1.
K-L divergence
The selection of relevant indicators is crucial to the effectiveness of constructed leading indicators. K-L divergence method, introduced by Kullback and Leibler (1951), provides a criterion for evaluating the similarity between probability distributions. The method varies the time lag between two target sequences, and finds out the minimum time lag. Recentely, K-L divergence is widely used to detect changes in input data across statistical and machine learning models. Jeomoan and Mohamed (2024) use it to identify shifts in data distribution over time in automated decision-making processes.
Note that a sequence (p={{p}_{i}{;i}ge 1}) satisfying ({p}_{i} ,>, 0) and (sum {p}_{i}=1) can be regarded as the probability distribution sequence of a random variable. Therefore, a distribution sequence p is obtained by normalizing the reference indicator sequence x as follows:
$${p}_{i}={x}_{i}/left(mathop{sum }limits_{i=1}^{n}{x}_{i}right)$$
(1)
Along a similar procedure, one can obtain another probability distribution sequence q by normalizing indicator sequence ({y}_{i}). The K-L divergence ({K}_{l}) between distributed sequences p and q is constructed in formula (2), which is used to describe the difference between indicator sequences x and y with different time differences
$${K}_{l}(p,,q)=mathop{sum}limits_{i=1}^{n}{p}_{i}left({mathrm{ln}}{p}_{i}-{mathrm{ln}}{q}_{i+l}right),l=0,pm 1,pm 2,ldots ,pm L$$
(2)
Compute the K-L divergence with various time differences ranging from −L to L, and choose the smallest one as the final result
$${K}_{l}^{{prime} }=mathop{min }limits_{-Lle lle L}{K}_{l}$$
(3)
The time difference l corresponding to the minimum K-L divergence is the optimal lag (leading) period of the evaluation index. The proximity of K-L divergence to zero indicates a higher degree of similarity between the two target sequences.
Index methods
Prosperity index
The prosperity index is constructed by combining relevant variables together to reflect the status from the set of quantifiable targets, which has been widely used by the U.S. Department of Commerce as well as the Japanese Economic Planning Agency Bureau of Investigation. The prosperity index is an indicator that summarizes the qualitative indicators in the industry through quantitative processing and comprehensively reflects the state and development trend of the research object. This article constructs the prosperity index to show the development level of digital economy as follows, one can also refer to Tu et al. (2016).
Through calculating the mean value μ and standard deviation σ of the indicators, set (mu pm sigma), (mu pm 3sigma) as the thresholds to judge the signal score of each indicator. The signal scores of the value ({I}_{{ij}}) of indicators are assigned 1 to 5 in the five ranges respectively from small to large and are added together to obtain the prosperity index (P{I}_{j})
$${S}_{ij}=left{begin{array}{ll}1,,{I}_{{ij}}le mu -3sigma ,\ ,2,,{mu -3sigma ,, mu +3sigma .end{array}right.$$
(4)
$$P{I}_{j}=mathop{sum }limits_{i=1}^{n}{S}_{ij}$$
(5)
Set quartiles 20%, 40%, 70%, and 85% of the upper limit as division of the prosperity intervals. Prosperity intervals are established by setting four boundary values and five intervals corresponding to five different states: the slow period, the relatively slow period, the stable period, the relatively prosperous period and the prosperous period.
Composite index
Composite index is constructed by combining the rate of change of the consistent, lagging and leading indicators to reflect the current developing status of the whole object industry (Chakrabartty, 2017). This paper establishes the composite index to show the development level of digital economy, one can also refer to Zhao and Xu (2023).
The symmetric rate of change of a single indicator is calculated and standardized by defining the i-indicator t-period data of j-group as ({Y}_{{ij}}(t)), (j=1,,2,,3), which denotes the consistent, leading and lagged groups respectively, and (i=1,,2,,.,.,.,,,{k}_{j}) is the indicator serial number within the indicator group, that is the number of indicators in the first group. Its symmetric rate of change is as follows:
$${C}_{{ij}},left(tright)=200times frac{,{Y}_{{ij}},left(tright)-{Y}_{{ij}},left(t,-,1right)}{{Y}_{{ij}},left(tright)+{Y}_{{ij}},left(t,-,1right)}$$
(6)
Then, obtain the following normalized symmetric rate of change,
$${S}_{{ij}}={(n-1)C}_{{ij}}times {left(mathop{sum }limits_{i=2}^{n}left|{C}_{{ij}}left(tright)right|right)}^{-1},t=2,3,ldots ,n$$
(7)
Next, calculate the standardized value of the average rate of the indicators in each group
$${R}_{j}left(tright)=left(mathop{sum }limits_{i=1}^{{k}_{j}}{S}_{{ij}}left(tright){W}_{{ij}}right)times {left(mathop{sum }limits_{i=1}^{{k}_{j}}{W}_{{ij}}right)}^{-1}$$
(8)
where (j=1,,2,,3), ({W}_{{ij}}) represents the weight of the i-th indicator in the j-th group.
The rate of change is taken to be the standardization factor is listed below:
$${F}_{j}=left(mathop{sum }limits_{t=2}^{n}left|{R}_{j}left(tright)right|/left(n-1right)right)times {left(mathop{sum }limits_{t=2}^{n}left|{R}_{i}left(tright)right|/left(n-1right)right)}^{-1}$$
(9)
where ({R}_{i}(t)) is the average rate of change of the consistent indicator group. Standardize mean rate of change as ({Vj}left(tright)={R}_{j}(t)/{F}_{j}). Set ({I}_{j}left(1right)=100), ({bar{I}}_{j}) as the base year mean, the initial synthetic index as
$${I}_{j}left(tright)={I}_{j}left(t-1right)times frac{200+{V}_{j}left(tright)}{200-{V}_{j}left(tright)}$$
(10)
and the Composite index is (C{I}_{j}left(tright)=left({I}_{j}left(tright)/{bar{I}}_{j}right)times 100).
Savitzy-Golay convolutional algorithm
The Savitzky-Golay convolutional smoothing algorithm, introduced by Simone et al. (2014), is an effective method for data smoothing and filtering. Sadıkoglu and Kavalcıoğlu (2016) demonstrate that it can effectively filter out various types of noise while preserving the shape of the data signal and maintaining the signal’s width. The formula is as follows
$$y={a}_{0}+{a}_{1}{x}_{1}+{a}_{2}{x}_{2}+{a}_{3}{x}_{3}+.,.,.,.,.,.+{a}_{k-1}{x}_{k-1}$$
(11)
where ({{a}_{n},{n}ge ,1}) is the parameter sequence. The value of a in the above equation is obtained by the least square method, and the fitted value is brought in and transformed into matrix form to solve the equations as the following formula
$$hat{A}={left({X}^{T}Xright)}^{-1}{X}^{T}Y$$
(12)
Thus, the filtered value of the model is obtained as follows
$$hat{Y}=Xleft({X}^{T}Xright){X}^{T}Y$$
(13)
Construction of Grey-Markov model
The Grey-Markov model is constructed based on the grey system theory (see, e.g., Li et al., 2015) and Markov theory, which can make up the shortcoming of grey model in predicting sequence fluctuations.
This research assumes that the residual sequence has a stable state transition probability and satisfies the Markov property. The assumption of short-term dependency in residuals in the Grey-Markov model is easier to meet when residuals are white noise sequences.
Grey prediction model uses the original data generation process to get the overall changes and generate a strong regularity of the data sequences, one can then construct different equation model to predict the trend. This model is established by treating the prediction sequence ({X}_{0}={{x}_{01},,{x}_{02},,.,.,.,,,{x}_{0n}}) accumulated to generate a one-time cumulative sequence ({X}_{1}={{x}_{11},,{x}_{12},,.,.,.,,,{x}_{1n}}), where
$${x}_{1k}=mathop{sum }limits_{i=1}^{k}{x}_{0i},,k=1,,2,,.,.,.,.,.,n$$
(14)
The first-order differential equation is established based on a primary cumulative sequence ({X}_{1}) as follows:
$$frac{d{X}_{1}}{{dt}}+{alpha }_{1}{X}_{1}={alpha }_{2}$$
(15)
where α is the grey development coefficient and q is the grey role quantity.
Write ({boldsymbol{a}}={left({alpha }_{1},{alpha }_{2}right)}^{T}), then apply the OLS method to obtain the parameter estimates
$$hat{{boldsymbol{a}}}={left(hat{{alpha }_{1}},hat{{alpha }_{2}}right)}^{T}={left({B}^{T}Bright)}^{-1}{B}^{T}{boldsymbol{d}}$$
(16)
where
$${boldsymbol{B}}=left[begin{array}{cc}-0.5left({x}_{11}+{x}_{12}right) & 1\ -0.5left({x}_{11}+{x}_{13}right) & 1\ vdots & vdots \ -0.5left({x}_{1(n-1)}+{x}_{1n}right) & 1end{array}right],{boldsymbol{d}}{{=}}left[begin{array}{c}{x}_{02}\ {x}_{03}\ vdots \ {x}_{0n}end{array}right]$$
(17)
$${hat{x}}_{1(k+1)}=left({x}_{01}-frac{hat{{alpha }_{2}}}{hat{{alpha }_{1}}}right){e}^{-hat{{alpha }_{1}}k}+frac{hat{{alpha }_{2}}}{hat{{alpha }_{1}}}$$
(18)
Let all ({hat{x}}_{1i}) in the sequence minus the previous value to restore the predicted value ({hat{x}}_{0i}), compute the residual sequence ({E}_{0}) and accumulate its absolute value to get a cumulative residual sequence
$$begin{array}{ll}{E}_{0}={|{e}_{01}|,|{e}_{02}|,ldots ,|{e}_{0,n}|}\quad,,=,{|{x}_{02}-{hat{x}}_{02}|,|{x}_{03}-{hat{x}}_{03}|,ldots ,|{x}_{0k}-{hat{x}}_{0k}|}end{array}$$
(19)
$${{{|}}e}_{1k}{{|}}=mathop{sum }limits_{i=1}^{k}{{{|}}e}_{0i}{{|}},,k=1,,2,,.,.,.,.,.,n$$
(20)
Grey prediction model is used to estimate the absolute value of the cumulative residual sequence, and on this basis, an estimate of the absolute value of the residual sequence is obtained, which is used to correct for ({hat{x}}_{0i}), it follows that
$${hat{e}}_{0k+1}={e}_{1k+1}-{hat{e}}_{1k+1}$$
(21)
$${hat{{x}^{{prime} }}}_{0k}={hat{x}}_{0k}+{m}_{0k}{hat{e}}_{0k+1}$$
(22)
where
$${m}_{0,k}=left{begin{array}{c}1,left({x}_{0k}-{hat{{rm{x}}}}_{0k}right)ge 0,\ -1,left({x}_{0k}-{hat{x}}_{0k}right)le 0.end{array}right.$$
(23)
Note that the positivity and negativity of ({m}_{0,k}) are random, therefore the Markov chain is used to compensate for the shortage of the traditional grey prediction model in prediction accuracy.
The method divided ({E}_{0}) into two states, of which state 1 means positive residuals, while state 2 denotes negative residuals. Define ({M}_{{ij}}) as the frequency from state i to j, and ({M}_{i}) as the total number of times for state i, the probability ({p}_{{ij}}) is defined as follows:
$${p}_{{ij}}={M}_{{ij}}times {{M}_{i}}^{-1},left(i,=,1,,2{{;}},j,=,1,,2right)$$
(24)
Thus, the transition matrix for states is given below
$$P=left[begin{array}{cc}{p}_{11} & {p}_{12}\ {p}_{21} & {p}_{22}end{array}right]$$
(25)
Account of the above procedures, the probability of each state can be obtained, and the largest probability of states will be selected to determine the value of ({m}_{0k}) in ({hat{X}}_{0k}).











Leave a Reply